Exponential and Logarithmic Functions
Objectives:
- Represents an exponential and logarithmic functions through its: table of values, graphs, and equations.
- Determine the relationship between exponential and logarithmic functions.
- Solve problems involving exponential and logarithmic functions.
Exponential and Logarithmic functions are important in both theory and practice. In this unit we look at the graphs and equation of these two functions to determine how they are related to each other.
_________________________________________________________________
1) Exponential Functions
Consider a function of f(x) = a^x, where a>0. Such a function is
called an exponential functions. We can take three cases, where a = 1, 0<a<1, and a > 1.
If a = 1 then,
f(x) = 1^x = 1
this just gives us a constant function f(x) = 1.
__________________________________________________________________
Then, what happen if a > 1? To test this case, take a numerical example, let a = 2.
f(x) = 2^x
f(0) = 2^0 = 1 f(-1) = 2^-1 = 1/2 or .5
f(1) = 2^1 = 2 f(-2) = 2^-2 = 1/4 or .25
f(2) = 2^2 = 4 f(-3) = 2^-3 = 1/8 or .125
f(3) = 2^3 = 8 f(-4) = 2^-4 = 1/16 or .0625
we can put these results into table, and plot a graph of the function.
http://wdmath8.weebly.com
The important properties of the graphs of these types of function are:
- f(0) = 1 for all values of a. This because a^o = 1 for any value of a.
- f(x) > 0 for all values of a. This because a > 0 implies a^x > 0.
______________________________________________________________
What happens if 0 < a < 1? To examine this case, take another numerical example. Suppose that a = 1/2.
f(x) = 1/2^x
f(0) = 1/2^0 = 1 f(−1) = 1/2^−1 = 2/1^1 = 2
f(1) = 1/2^1 = 1/2 f(−2) = 1/2^−2 = 2/1^2 = 4
f(2) = 1/2^2 = 1/4 f(−3) = 1/2^−3 = 2/1^3 = 8
f(3) = 1/2^3 = 1/8
We can put these results into a table, and plot a graph of the function.
http://moodle.oakland.k12.mi.us/
_________________________________________________________________
2) Logarithmic Functions 
We shall now look at logarithm functions. These are functions of the form f(x) = 
where a > 0. We do not consider the case a = 1, as this will not give us a valid function.
What happens if a > 1? To examine this case, take a numerical example. Suppose that a = 2. Then,
f(x) = 
means 
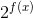= x.
An important point to note here is that, regardless of the argument, 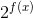> 0. So we shall consider only positive arguments.
f(1) = 
means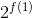 
= 1 so f(1) = 0
f(2) =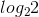 
means 
= 2 so f(2) = 1
f(4) = 
means 
= 4 so f(4) = 2
f( 1/2 ) = 
means 
= 1/2 = 2^−1 so f( 1/2 ) = −1
f( 1/4 ) = 
means 
= 1/4 = 2^−2 so f( 1/4 ) = −2
We can put these results into a table of values, and plot a graph of the function.
http://www.smtutor.com/
The important properties of the graphs of these types of functions are:
- f(1) = 0 for all values of a;
- we must have x > 0 for all values of a.
_________________________________________________________________
3) The relationship between Exponential and Logarithmic Function
We can see the relationship between exponential function f(x) = e^x and the logarithm function f(x) = ln x by looking at their graphs.
We can straight away that the logarithm function is a reflection of exponential function in the line represented by f(x) = x. In other words, the axes have been swapped: x becomes f(x). and f(x) becomes x.
KEY POINTS:
The exponential function f(x) = e^x is the inverse of the logarithm function f(x) = ln x.
Powered by:
-MTAQ
Relationship between Exponential and Logarithmic Functions 